(x y)^3 identity 105276-(x+y)^3 identity class 9

(i) To prove x 3 y 3 = (x y) (x 2 – xy y 2) Now, using identity VI we can say (x y) 3 = x 3 y 3 3xy (xy) Or, (xy) 3 – 3xy (x y) = x 3 y 3 Or, x 3 y 3 = (x y) {(xThis video shows how to expand using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuseriesaWhat I hope to do in this video is prove the angle addition formula for sine or in particular prove that the sine of X plus y X plus y is equal to is equal to the sine of X sine of X times the cosine of sine of I forgot my X sine of X times the cosine of Y times the cosine of y plus cosine of X cosine of X times the sine of Y times the sine of Y and the way I'm going to do it is with this

Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

(x+y)^3 identity class 9

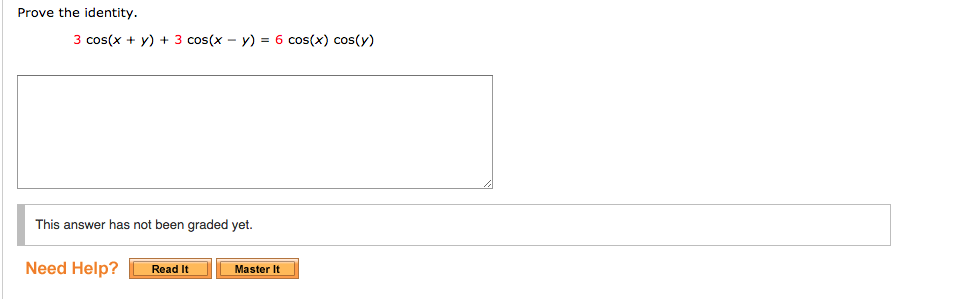
(x+y)^3 identity class 9-Prove the identity sin( 1 x) = sin(3 x) Question Prove the identity 3 cos(x y) 3 cos(x y) = 6 cos(x) cos(y) Use a Reciprocal Identity, and then rewrite as a single rational expression 7 tan(x) 7 tan(y) = 7 sin(y) cos(y) cos(x) = cos(x) cos(y) Use an Addition or Subtraction Formula to simplify Prove the identity sin( 1 x(9) Verify (i) x 3 y 3 = (x y) (x 2 − xy y 2) (ii) x 3 – y 3 = (x − y) (x 2 xy y 2) using some nonzero positive integers and check by actual multiplicationCan you call these as identites ?

1

Y = b Using the values of x &Identity function is a function which gives the same value as inputtedExamplef X → Yf(x) = xIs an identity functionWe discuss more about graph of f(x) = xin this postFind identity function offogandgoff X → Y&Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text 5 Set up a table and verify the identity for the given values of x and y (10) tan1 (x) tan1 (y) = 1 tan1 x = 1, y = v3 xy 9 1xy

Z (iii) 56 mn 2 p 2 = 2 ×Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy• for every y ∈ Y, then map φy X 3 y 7−→φ(x,y) ∈ K is conjugate linear, ie the map X 3 x 7 This case is a particular instance of the Polarization Identity discussed in Remark 31 Corollary 31 Let X be a Kvector space equipped with an inner product

Using identity, (x y z)2 2= x 2 y z2 2xy 2yz 2zx We can say that, x 2 2 y z 2xy 2yz 2zx = (x y z) 2 4x 2 9y 16z12xy–24yz–16xz =(2x) 2 (3y) 2 (−4z) 2 (2×2x×3y)(2×3y×−4z)(2×−4z×2x)Identify the inner function u = 9(x) and the outer function y = f(u) (Use nonidentity functions for fu) and g(x)) y revi (u), g(x)) dy Find the derivative dx ic dy dx 2() Need Help?Find the value of 533 using the identity (x y)3 = x3 3x2y 3xy2 y3 Hint 533 = (50 3)3;

Solved Prove The Identity 3 Cos X Y 3 Cos X Y 6 Chegg Com

Identity Vs Equation Acute Angel

Mathematics RS Agarwal Standard IX Q 1 Expand each of the following, using suitable identities (i) ( x 2 y 4 z) 2 (ii) ( 2 x − y z) 2 (iii) ( − 2 x 3 y 2 z) 2 (iv) ( 3 a − 7 b − c) 2 (v) ( − 2 x 5 y − 3 z) 2 (vi) 1 4 a − 1 2 b 1 2Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the other(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yz

What Is The Answer Of X Y Quora

Pdf Antiflexible Rings With Identity X Y X 0 M Hema Prasad Academia Edu

Given For all real numbers x and y such that x y = 3, the following identity hold axy bxcy 9 = 0 To find Value of a b c Solution For all real numbers x and y such that x y = 3, the following identity hold axy bxcy 9 = 0Dissociative identity disorder (DID), previously known as multiple personality disorder (MPD), is a mental disorder characterized by the maintenance of at least two distinct and relatively enduring personality states The disorder is accompanied by memory gaps beyond what would be explained by ordinary forgetfulness The personality states alternately show in a person's behavior;(ii) 36 x 3 y 2 z = 2 ×

Bedow Bedow Nunchi Branding And Strategy

If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 7 Y 3 X 2 49 Y 2 9 X Y 21

Videos 251 Syllabus Concept Factorisation using Identity a3 b3 = (a b)(a2 ab b2)The cosine of a compound angle a plus b is expressed as cos ( a b) in trigonometry The cosine of sum of angles a and b is equal to the subtraction of the product of sines of both angles a and b from the product of cosines of angles a and b This mathematical equation is called the cosine angle sum trigonometric identity in mathematicsNotice that if we add or multiply two whole numbers, the result is another whole number However, if we subtract two whole numbers, the result is not necessarily another whole number 5 7 =

Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8

If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 7 Y 3 X 2 49 Y 2 9 X Y 21

Identity VIII a 3 b 3 c 3 = 27x 3 – 64y 3 – 108x 2 y 144xy 2 Example 5 Factorize (x 3 8y 3 27z 3 – 18xyz) using standard algebraic identities Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z So we have,X x y y is a right identity Then, for all M = a a b b 2S we have that a a b b x x y y = a a b b Multiplying the left hand side we get, ax ay ax ay bx by bx by = a a b b Equating the entries of the matrices leaves the equations ax ay = a and bx by = b ByThe Baker–Campbell–Hausdorff formula supplies the necessary correction terms Transcendency The function e z is not in C(z) (that is, is not the quotient of

Learn Algebraic Identities Of X Y And X Y In 3 Minutes

Pdf On The Identity Of Fermat S Equation

403 Authorization Error This server could not verify that you are authorized to access the document requested If you feel you have reached this page in errorGet FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Exercise 25 We have created Step by Step solutions for Class 9 maths to help you to revise the complete Syllabus and Score More marksUse the identity (xy)(x^2−xyy^2)=x^3y^3 to find the sum of two numbers if the product of the numbers is 28, the sum of the squares is

What Is The Formula Of Math A B 3 Math Quora

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are ⁡ (), ⁡ (), and ⁡ (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, ⁡ and ⁡, if an interpretation is unambiguously possible The sine of an angle is definedFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, theExpert Answer Who are the experts?

1

How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

The identity exp(x y) = exp x exp y can fail for Lie algebra elements x and y that do not commute;Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)Click here👆to get an answer to your question ️ x^3 y^3 = (x y)(x^2 xy y^2) prove this identity

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9

C The identity transformation is the map Rn!T Rn doing nothing it sends every vector ~x to ~x A linear transformation T is invertible if there exists a linear transformation S such that T S is the identity map (on the source of S) and S T is the identity map (on the source of T) 1 What is the matrix of the identity transformation?Xy 2 cos x y 2 sinx siny= 2sin x y 2 cos xy 2 cosx cosy= 2cos xy 2 cos x y 2 cosx cosy= 2sin xy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A The height of the triangle is h= bsinA Then 1If a<h, then ais too short to form a triangle, so there is no solutionLy ≡ l(x)y′′ p(x)y′ q(x)y= l(x)y′ ′ q(x)y (59) A general operator L may not be selfadjoint but it can always be converted into a selfadjoint by suitably multiplying L with a function Lemma 53 (selfadjointisation) The operator h(x)Ly is selfadjoint, where his given by h(x) = 1 l(x) exp ˆZ x p(t) l(t) dt ˙ (510) In

Experiment No 2 Boolean Algebra

Ex 9 5 3 Find The Squares Xy 3z 2 Using The Algebra Identities

X y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2While it is possible to solve for A A A and B B B, a more elegant solution exploits the identity (x y) 3 = x 3 3 x 2 y 3 x y 2 y 3, (xy)^3 = x^3 3x^2y 3xy^2 y^3, (x y) 3 = x 3 3 x 2 y 3 x y 2 y 3, which can be rewritten as x 3 y 3 =0(x−y,t)ϕ(0,y)∆0(x−y,t)ϕ t(0,y) dy (15) with ∆0(x−y,t)≡ 1 2 θ y−(x−t) −θ y−(xt) (161) ∇ 0(x−y,t)≡ 1 2 δ y−(x−t) δ y−(xt) (162) =∂ ∂t ∆ 0(x−y,t) Itisimportanttonoticethat,whilewehadprediction (ie,evolutionfrom prescribedinitial data)inmindwhenwedevised(15),theequationalsoworks retrodictively

Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community

Algebraic Identities Of Polynomials A Plus Topper

Remark 32 Note that an identity (left or right or both) for one operation does not have to be an identity for another operation Think of addition and multiplication let x be an integer Let y be a right inverse of x Then x ∗ y = 1 That is, xy −1 = 1 Solving for y we find y = −x2Answer (1 of 3) A classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, x^3 y^3 z^3 3xyz = (xyz)(x^2y^2z^2xyyzzx)(1) As x, y &Prove the identity Key Show your work cot(x y) = cot y cot x − 1 cot y cot x 17 Question Details SPreCalc6 Find sin 2 x, cos 2 x, and tan 2 x from the given information sin 2 x= cos 2 x= tan 2 x= tan x = − , x in Quadrant II 15 8

1

X 3 Y 3 X 3 Y 3 Formula Proof Youtube

Practice with the properties of real numbers The word NUMBERS implies the answer will deal only with numbers The word X implies the answer will contain a variable, but not necessarily the variable x A B Distributive Property (Numbers) 3 (5 2) = 15 6 Commutative Property of Addition (Numbers) 3 7 = 7 3Z are positive numbers, (xyz) >Therefore, x = 50 and y = 3 I dont get this at all?

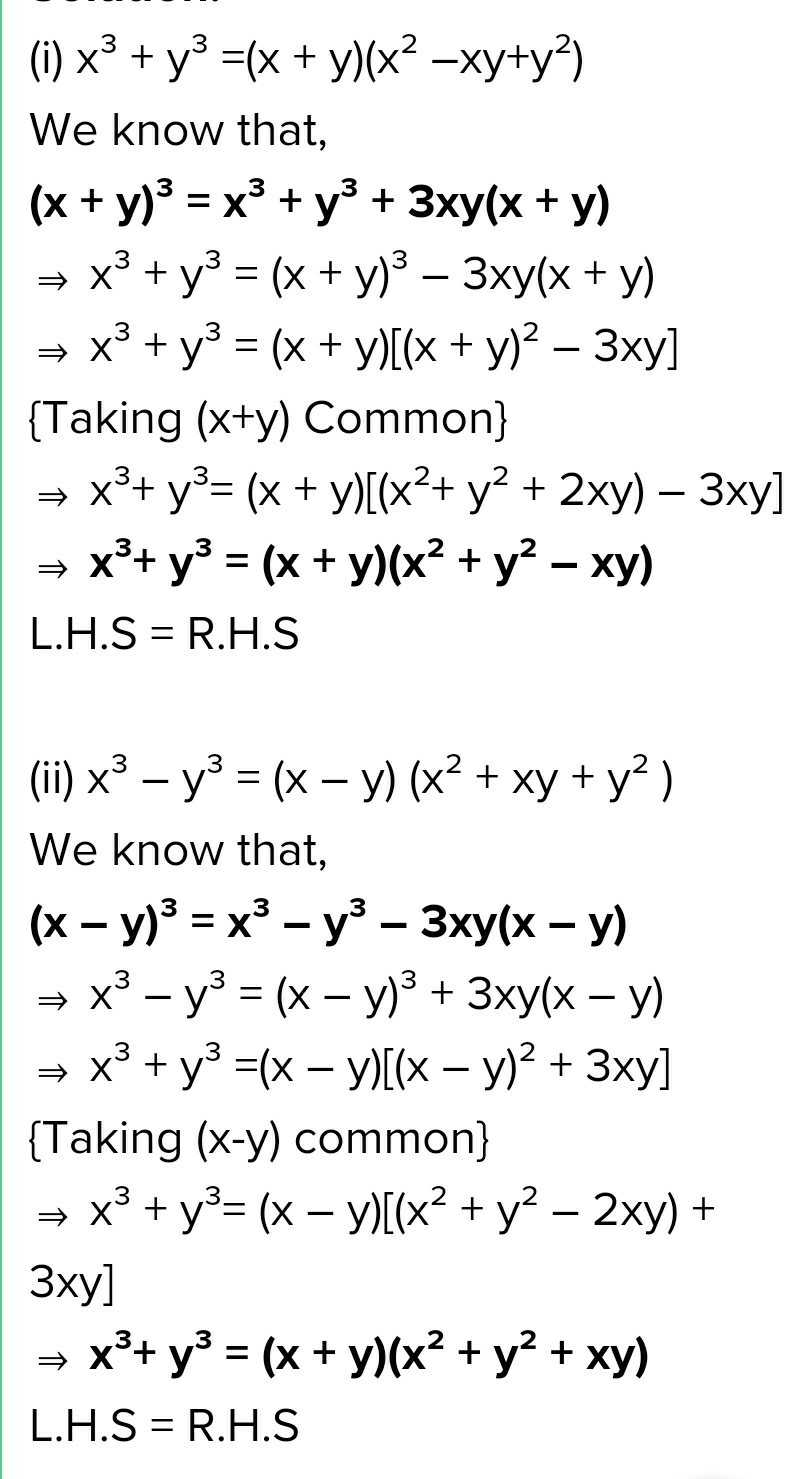
9 Verify I X3 Y3 X Y X2 Xy Y Ii P X Y X2 Xy Scholr

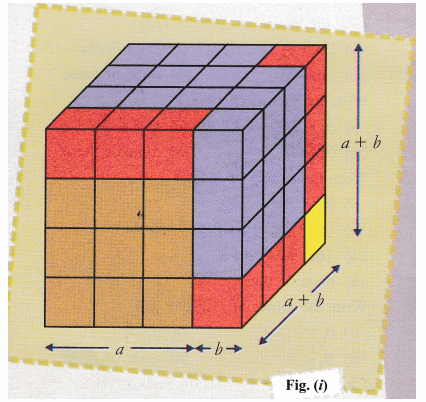
Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers

Simplify (X Y)3 − (X − Y)3 Maharashtra State Board SSC (English Medium) 8th Standard Textbook Solutions 3717 Important Solutions 1 Question Bank Solutions 1905 Concept Notes &Called an identity element with respect to if e x = x = x e for all x 2A Example 1 1 is an identity element for multiplication on the integers 2 0 is an identity element for addition on the integers 3 If is de ned on Z by x y = x y 1 Then 1 is the identity 4 The operation de ned on Z by x y = 1 xy has no identity elementG Y → Xgofgof= g(f(x))gof X → XWe input xSo, we should get x∴gof= xWe writegof= IXwhe

Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5

Answered Prove The Polynomial Identity For The Bartleby

Comparing the polynomial with the identity we have, x = 3 a &Read Watch it Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorP Question 4 Using the identity (x a)(x b) – x 2 x(a b) ab, find the following product (i) (x 3) (x 7) (ii) (6a 9) (6a – 5) (iii) (4x 3y) (4x 5y) (iv) (8 pq) (pq 7) Solution (i) (x 3

Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks

How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com

The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3Use the identity x3y3z3−3xyz=(xyz)(x2y2z2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xyyzzx) is 107(x y) 3 = x (y 3) Associative Property of Multiplication (6x)y = 6(xy) Additive Identity y 0 = y Additive Inverse b (b) = 0 Multiplicative Identity x(1) = x Multiplicative Inverse x(1/x) = 1 Reflexive Property 5 = 5 Symmetric Property If x 6 = 8, then 8 = x 6 Symmetric Property If a = 7, then 7 = a Transitive

X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55

Darlene Wrote This Proof Of The Identity X Y 2 X Y 2 4xy Which Of The Following Is A Justification For Step 5 Of

Y, other terms of the polynomials are written as shown Since, x 3 3 x 2 y 3 x y 2 y 3 = (x y) 3 Let's factorize another polynomial This has both positive and negative terms, so it can be compared with the expansion of (xAnswer (1 of 16) Mentally examine the expansion of (xyz)^3 and realize that each term of the expansion must be of degree three and that because xyz is cyclic all possible such terms must appear Those types of terms can be represented by x^3,

Algebraic Identities 6 And 7 Youtube

Solved Prove The Identity 3 Cos X Y 3 Cos X Y 6 Cos X Chegg Com

Ex 9 2 5 Class 8 Obtain The Product Of I Xy Yz Zx Teachoo

Solved V Boolean Algebra 1 Derive This Identity X X Y Chegg Com

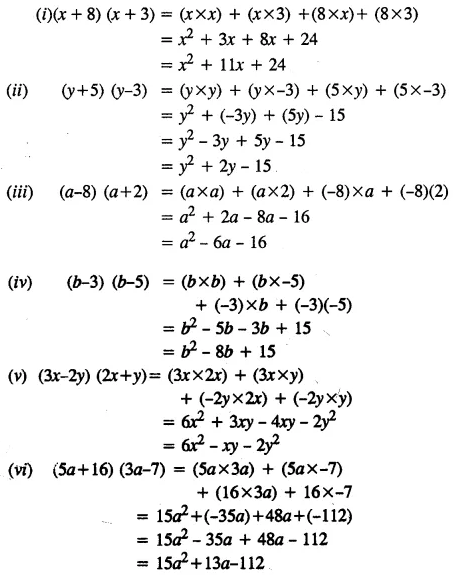
Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts

Pdf On Trace Forms On A Class Of Commutative Algebras Satisfying An Identity Of Degree Four

Learn Algebraic Identities Of X Y And X Y In 3 Minutes

Solved Questions 1 Demonstrate By Means Of Truth Tables Chegg Com

Factorise 27 X Y 3 8 X Y 3 Maths Polynomials Meritnation Com

Cos X Y 3 Verify The Identity 1 Tan X Tany Chegg Com

Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo

Using Identities Prove That X Y Z 2 Is Greater Than Or Equal To 3 Xy Yz Zx Maths 419 Meritnation Com

Ppt Polynomials Powerpoint Presentation Free Download Id

If X Y 26 And Xy 3 Find The Value Of X Y 4y 2 A A 4yi If 26 And 3 Maths Algebraic Expressions And Identities Meritnation Com

Solved 3 Simplify The Following Functional Expressions Chegg Com

Expert Answer What Are The Factors Of X Y 3 X3 Y3 Brainly In

Algebraic Identities Of Polynomials A Plus Topper

Find The Following Squares By Using The Identities I B 7

Get The Right Pair Of Algebraic Identities A B A X Y 2 1 X Y X2 Y2 Xy B X2 Y 2 2 Brainly In

Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8

Use A Suitable Identity To Fi See How To Solve It At Qanda

List Of Trigonometric Identities Wikipedia

1

Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In

Find The Following Squares By Using Identities I B 7 2 Ii Xy 3z 2 Sarthaks Econnect Largest Online Education Community

Koreascience Or Kr

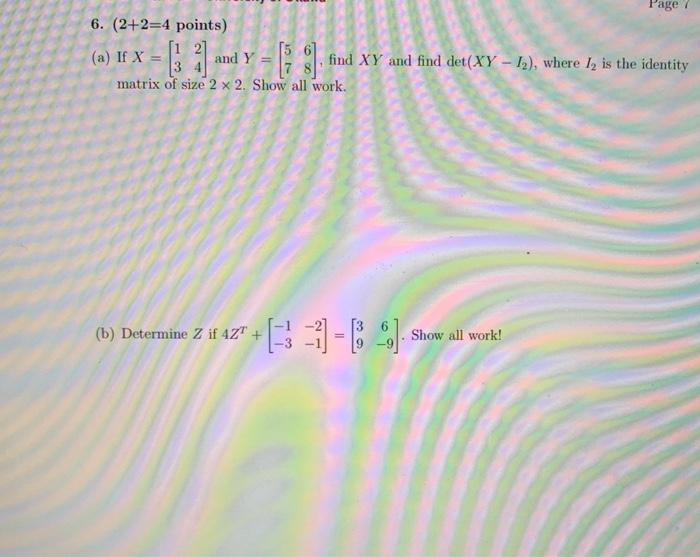
Solved Page 6 2 2 4 Points 1 27 56 A If X And Y 3 Chegg Com

Ppt Polynomials Powerpoint Presentation Free Download Id

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Example 11 Using Identity I Find 2x 3y 2 Algebra Class 8

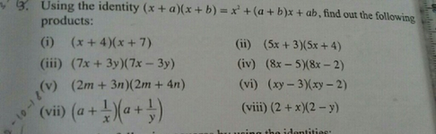
V3 Using The Identity X A X B X A B X Ab Find Ou Scholr

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Companion Website Example Of Information Displayed If The Identity Download Scientific Diagram

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

How To Expand Using The Identity Xy 3 X3 Y3 3x2y 3xy2 Youtube

How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Rational Functions And Endomorphisms Separable Endomorphisms Parallelogram Identity And Degree Map

Learn Algebraic Identities Of X Y And X Y In 3 Minutes

Exponentiation Wikipedia

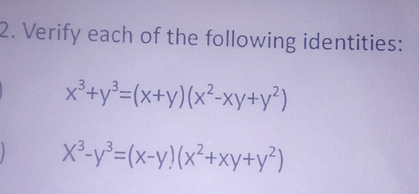
2 Verify Each Of The Following Identities X3 Y3 X Y X2 X Scholr

Learn Algebraic Identities Of X Y And X Y In 3 Minutes

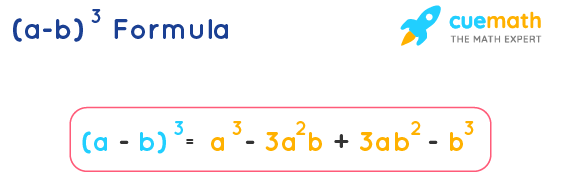
A Minus B Whole Cube Formula Examples A B 3 Formula

Algebraic Identities Of Polynomials A Plus Topper

Identity Mathematics Wikipedia

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Solved Prove The Identity Sin X Y Sin X Y 2 Cos X Chegg Com

Arxiv Org

Maths Identity 8 Polynomial Part 12 English Youtube

2 Solve It Plz Q If X Y 10 And Xy 21 Find The Value Of X3 Y3 Using Identity Maths Polynomials Meritnation Com

Chapter 7 Spectral Theory Of Linear Operators In Normed Spaces

X Y 3 2 X Y 3 2 Solve By Using Suitable Identity Brainly In

Polynomials Ppt Video Online Download

Cos X Y Formula Proof Iventania

Math Garden Binomial Identity

Which Is A Polynomial Identity A X3 Y3 X Yx2 Xy Gauthmath

1

153 Pm Lte 404 1 D D Df See How To Solve It At Qanda

Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com

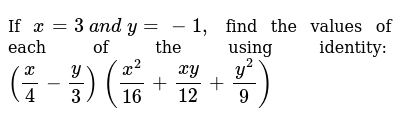
If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 4 Y 3 X 2 16 X Y 12 Y 2 9

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Given A X 3 Y 3 If A 3i Where I Is The Identity Matrix Of Order 2 Find X And Y Brainly In

Solved Question 3 We Want To Prove That For All X Y Cu Chegg Com

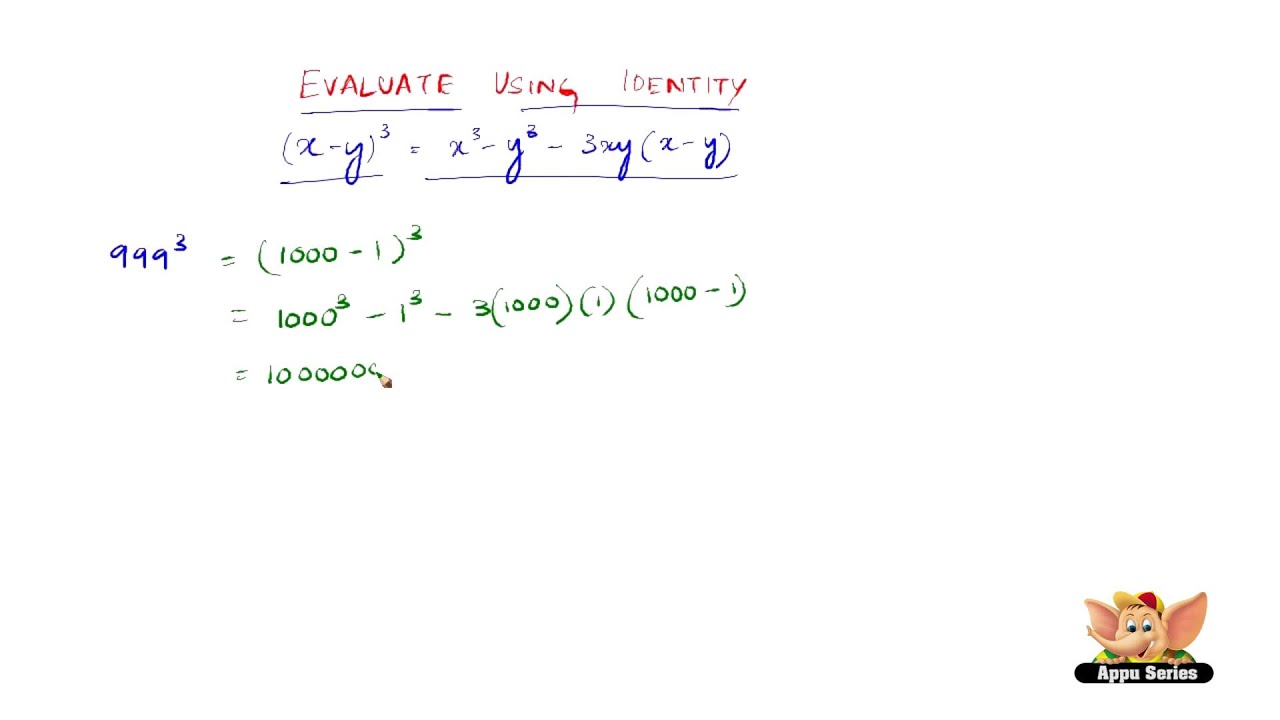
How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Entering Identities And The Problem Type Download Scientific Diagram

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials

Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8

Verify X Y 3 X3 Y3 3xy X Y Brainly In

Topperlearning Com

Incoming Term: (x+y)^3 identity, (x+y)^3 identity class 9, (x+y+z)^3 identity, complete the identity (x+y)^3,